SPC及CPK基本原理浅谈[转]

 SPC：Statistical Process Control------统计制程控制

    应用统计技术对过程中的各个阶段进行评估和监控，从而保证产品与服务满足要求的一种质量技术。

    先聊几个概念：

    正态分布（Normal distribution）:

    又名高斯分布（Gaussian distribution），一种最常见的连续性随机变量的概率分布，最早由棣莫弗（Abraham de Moivre）在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。

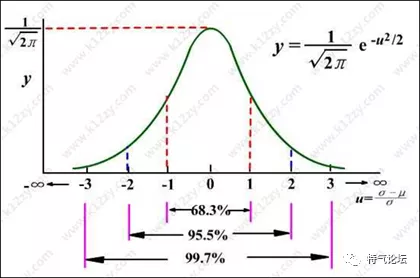
    是不是很纠结，看不懂，没关系。通俗来说正态分布是一个概率学的理论，是一种在某个精度前提下，多次重复导致的实际数值和平均值之间的分布状况。举例说明

• 手枪打靶，开枪10000次，对于正常人来说，靶纸着弹点的密度通常是越靠近靶心越多，距离靶心越远的着弹点越少（前提：平均打到靶心）。

• 高中学生平均身高172cm，通常来说靠近172cm的人数最多，越远离172cm，人数会越少。只要统计的取样足够，基本不会出现一个班级49%的同学身高高于185cm，49%同学身高低于155cm，只有2%同学的身高在172cm左右这种情况，这就是正态分布。

• 最后强调下，正态就是Normal，就是正常状态的意思，不能用杠精的思路去思考。

正态分布告诉我们，世间 万物，只有有足够的取样数据，分析后发现皆 有一定分布规律 。类似中庸之道，类似大数据，类似大家都喜欢去人多的地方，类似你老婆发脾气的时候你十有八九会怂。

    标准差（Standard Deviation） 

    是离均差平方的算术平均数（即：方差）的算术平方根，用σ表示。标准差也被称为标准偏差，或者实验标准差，在概率统计中最常使用作为统计分布程度上的测量依据。

    标准差是一组数据平均值分散程度的一种度量。一个较大的标准差，代表大部分数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。

    例如，两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ，但第二个集合具有较小的标准差。

标准差的意义是什么呢？简单来说就是说明取样数据的 离散程度 ，举例说明

• 全员集合：很集中的在一起：标准差小；很分散的站着：标准差大。

• 100次打靶，最差的是3环：标准差小；0-10环甚至脱靶都有：标准差大

知道前两个概念，敲黑板，说重点 ：正态分布符合以下规律

• 有68.2%数值位于平均值1个标准差的范围之内

• 有95.4%的数值位于2个标准差的范围以内

• 还有99.7%的数值位于3个标准差的范围以内

    只要 三个标准差 基本上可以做人上人了，同志们，简称3σ ：sigma

    是不是感觉有点傻，或者感觉自己不服，但这个不重要，这就是统计学的基础之一。

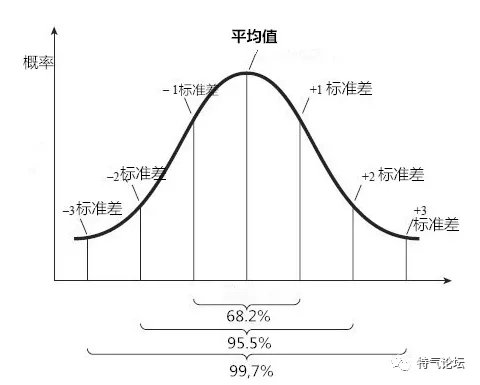
然后导入SPC概念，首先取得足够多的数据

开始画图

• 横坐标：以随时间推移而变动的样品号

• 纵坐标：控制参数或统计值

• 中心线（CL）：Central Line；代表实际数据平均值

• 上规格限（USL）：Upper Specification Line；代表规格/标准上限

• 下规格限（USL）：Upper SpecificationLine；代表规格/标准下限

• 上控制限（UCL）：Upper Control Line；代表数据控制的上限：3σ

• 下控制限（LCL） ：Lower Control Line；代表数据控制的下限：3σ

先搞UCL/LCL

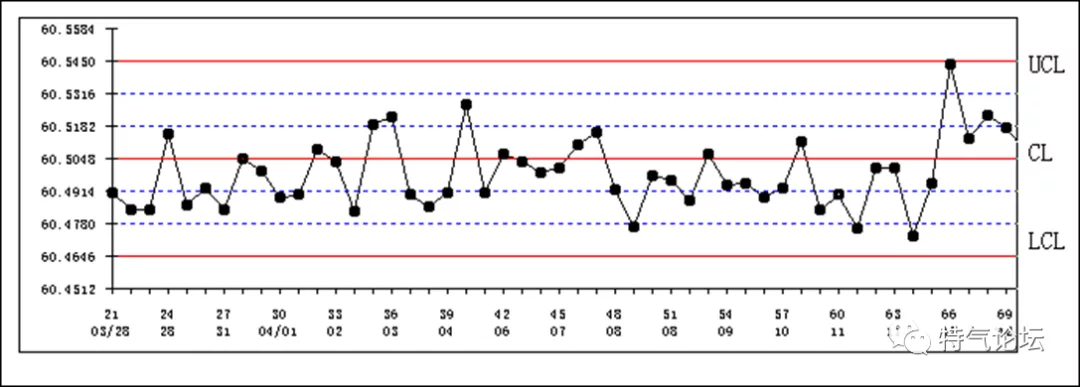
再搞USL/LSL

    只要确保USL/LSL在UCL/LCL的外侧，是不是就能保证合格率>99.7%？

答：是的，absolutely 是的！

    SPC的判断标准是什么呢？ 

    需要依据自己的行业特点和制程管控能力制定，普世的规律如下：

    OOC Rule

     所以结论是：只有确保平均值上下各设置3σ的范围在规格的正负偏差内，就可以确保合格率>99.7%。

    对于一般工业而言，>99.7%已经是很好的合格率了。如果确保USL-LSL远远大于UCL-LCL，是不是可以提高合格率，答：是的！

    上文谈了只要(USL-LSL)>大于(UCL-LCL)，就可以确保较高的合规率，但是精明的读者会发现一个问题，合格率是提高了，但是不能确保合格的产品都靠近我们的目标值或者靶心位置。

    下面两个SPC的Data 一样，都很好，但是大家会发现左图的Data无法接受，为什么呢？SPC中其实没有关注到Target也就是目标值或者靶心。

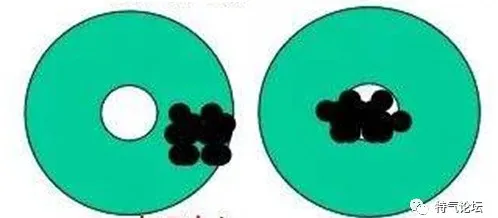
    怎么办？别急，还有CPK。

Cp:生产过程的自然能力与要求规格的比较

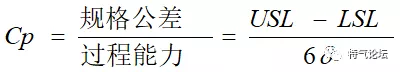
    CP啥意思？就是你的USL-LSL和三个西格玛的比例关系，越大说明你的制程控制能力越好，很简单，不容易出现不合格产品吗。

Cp指标的判断（Cp越大越好）：一般来说

• Cp<1，过程能力不足

• 1 ≤ Cp < 1.33，过程能力尚可

• 1.33≤ Cp < 1.67，过程能力充足

    大多数情况下：Mean≠Target，那么分析过程能力的时候就要考虑均值Mean的影响，所以就引入Cpk概念

    Cpk ：过程输出均值与规格中心或目标不重合时的过程能力指数

Cpk计算公式一：Cpk=(1-Ca) ×Cp

Cpk计算公式二: 

    CPK的意义：Target目标值和USL或LSL之间距离最小的那个，和3σ的比值，越大说明目标值越靠近平均值，说明越好。

SPC和CPK简单来说：

• SPC控制精度，简单来说打靶是不是比较集中，不手抖

• CPK控制准度，简单来说打靶是不是都比较靠近靶心，不歪眼

    打靶又精又准，是不是质量就高，是的，就是这样。

    要想质量稳而准，不手抖@SPC，不歪眼@CPK。

附图：精度和准度的不同状况 - 网络图

注：少量内容来自网络，如有侵权请告知，谢谢